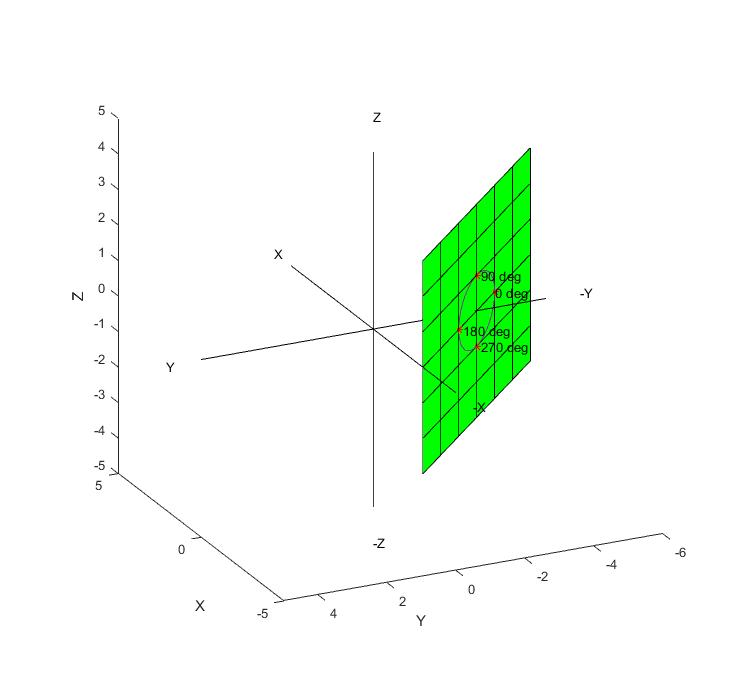
رشد مستطیل در یک مسیر سینوسی روی یک صفحه فضایی
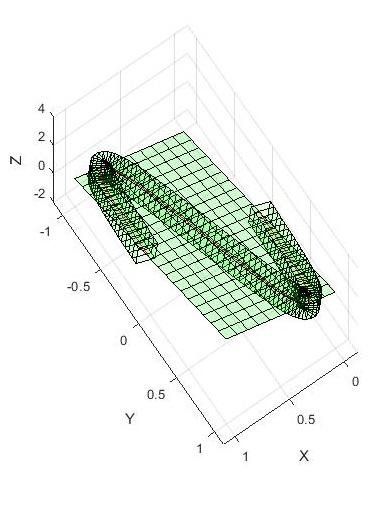
شما می توانید با تغییر معادله صفحه زیر در سط 4،نمودار سه بعدی رشد یافته روی مسیر را روی آن صفحه مشاهده کنین.
f(p,q)=2*p +2*q;
مثلا می توانین معادله صفحه در سط 4 را به فرم 2+ f(p,q)=2*p +0.5*q; تغییر دهین و نتیجه را مشاهده کنین.
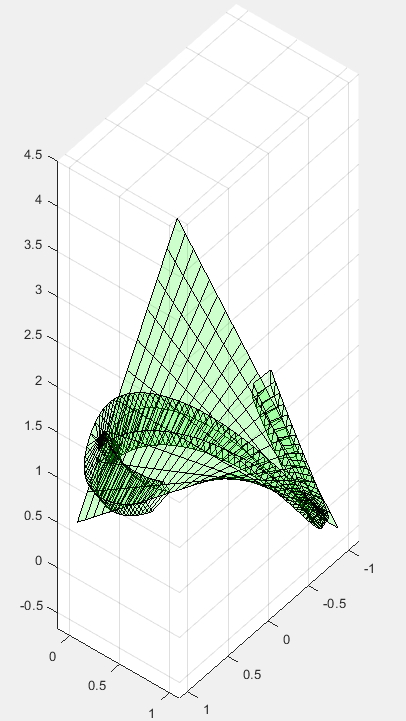
حتی می تونین، به جای صفحه معادله یک رویه را وارد کنین، مثلا سطر 4 را با معادله رویه f(p,q)=2*p +.5*q+2*p*q; جایگزین کنین. و نتیجه شکل زیر را مشاهده کنین.
کد اجرایی:
clc;
clear;
close all;
syms p q X Y Z yd(X) yl(X) f(p,q) ft(p,q) T xp(T) yp(T) zp(T)
f(p,q)=2*p +2*q;
[p1,q1]=meshgrid( 0:.1:1 ,-1:.1:1 );
surf(p1,q1,double(f(p1,q1)),FaceColor='g');alpha(.2);hold on;
t=linspace(0,1,100);
x=t;
y=sin(2*pi*x);yprim=2*pi*cos(2*pi*x);
plot3(x,y,f(x,y),'-r');hold on
n=length(t);
t1=linspace(0,1,200);
r=.08;
x1=r*sin(2*pi*t1);
y1=r*cos(2*pi*t1);
xM=[];
yM=[];
zM=[];
for s=1:length(t) -1
%plot equLine for slop and its 90 slop lines
%%
% yprims =double((y(s+1)- y(s))/(x(s+1)- x(s)));
yd(X)=yprim(s)*(X-x(s))+y(s);
yl(X)=(-1./yprim(s))*(X-x(s))+y(s);
tr=[x(s),x(s)+.00005 ];
d1=diff( double(tr));
d2=diff( double(yd(tr)));
d3=diff( double(f(tr,yd(tr))));
rd=[d1,d2,d3];
xp(T)=x(s)+rd(1)*T;
yp(T)=y(s)+rd(2)*T;
zp(T)=double(f(x(s),y(s)))+rd(3)*T;
tr1=double(solve((xp-x(s))^2+(yp-y(s))^2-r^2,T));
% plot3(xp(tr1),yp(tr1) ,zp(tr1),'b-' );hold on
%%
d1=diff( double(tr));
d2=diff( double(yl(tr)));
d3=diff( double(f(tr,yl(tr))));
r2=[d1,d2,d3];
% r2=[1,double(yl(x(s)+1))-double(yl(x(s))),double(f(x(s)+1,double(yl(x(s)+1))))-double(f(x(s),double(yl(x(s)))))];
xl(T)=x(s)+r2(1)*T;
yl(T)=y(s)+r2(2)*T;
zl(T)=double(f(x(s),y(s)))+r2(3)*T;
tr2=(double(solve((xl-x(s))^2+(yl-y(s))^2-r^2,T)));
% plot3(double(xl(tr2)),double(yl(tr2)) ,double(zl(tr2)),'c-' );hold on
df=(double((yprim(s))))/abs(double((yprim(s))));
if df==-1
tr2=tr2(end:df:1);
end
%%
% plot3(x1+x(s),y1+y(s) ,double(f(x1+x(s),y1+y(s))),'b-' );hold on
%%
r3=double([subs(gradient(f ),[p,q],[x(s),y(s)])',-1]);
xr=double(xl(tr2));
yr=double(yl(tr2));
zr=double(zl(tr2));
xr0(T)=xr(1)+r3(1)*T;
yr0(T)=yr(1)+r3(2)*T;
zr0(T)=zr(1)+r3(3)*T;
xr1(T)=xr(2)+r3(1)*T;
yr1(T)=yr(2)+r3(2)*T;
zr1(T)=zr(2)+r3(3)*T;
tr3=[-.02,.02];
% plot3(double([xr0(tr3),xr1([tr3(2),tr3(1)]),xr0(tr3(1))]),double([yr0(tr3),yr1([tr3(2),tr3(1)]),yr0(tr3(1))]),double([zr0(tr3),zr1([tr3(2),tr3(1)]),zr0(tr3(1))]));hold on
% plot3(xr0(tr3),yr0(tr3),zr0(tr3),'*')
xM=[xM;double([xr0(tr3),xr1([tr3(2),tr3(1)]),xr0(tr3(1))])];
yM=[yM;double([yr0(tr3),yr1([tr3(2),tr3(1)]),yr0(tr3(1))])];
zM=[zM;double([zr0(tr3),zr1([tr3(2),tr3(1)]),zr0(tr3(1))])];
% peripendecular plane
% peripendecular passpoints
rpX=diff(double(xl(tr2))');
rpY=diff(double(yl(tr2))') ;
rpZ=diff(double(zl(tr2)'));
B=[rpX,rpY,rpZ] ;
C=double([subs(gradient(f ),[p,q],[x(s),y(s)])',-1]);
C=cross(B,C);
refPlane=C(1)*(X-x(s ))+C(2)*(Y-y(s))+C(3)*(Z-f(x(s ),y(s))) ;
verPlaneCoff='XYZ';
[~,ind]=find(C);
ind=ind(end);
in=find(~ismember([1,2,3],ind));
ft(p, q)=subs(refPlane-C(ind)*sym(verPlaneCoff(ind)),[sym(verPlaneCoff(in(1))),sym(verPlaneCoff(in(2)))],[p,q]);
ft=-(ft/C(ind));
plot3(double([xr0(tr3),xr1([tr3(2),tr3(1)]),xr0(tr3(1))]),double([yr0(tr3),yr1([tr3(2),tr3(1)]),yr0(tr3(1))]),double([zr0(tr3),zr1([tr3(2),tr3(1)]),zr0(tr3(1))]),'r');hold on
% surf(double([xr0(tr3);xr1(tr3)]),double([yr0(tr3);yr1(tr3)]),double([zr0(tr3);zr1(tr3)]),FaceColor='g');hold on
% surf(double([xr0(tr3);xr1(tr3)]),double([yr0(tr3);yr1(tr3)]),double(ft(double([xr0(tr3);xr1(tr3)]),double([yr0(tr3);yr1(tr3)]))),FaceColor='b');hold on
plot3(double([xr0(tr3);xr1(tr3)])',double([yr0(tr3);yr1(tr3)])',double(ft(double([xr0(tr3);xr1(tr3)]),double([yr0(tr3);yr1(tr3)])))','b');hold on
plot3(double([xr0(tr3);xr1(tr3)]),double([yr0(tr3);yr1(tr3)]),double(ft(double([xr0(tr3);xr1(tr3)]),double([yr0(tr3);yr1(tr3)]))),'b');hold on
view(3)
xlabel('X');
ylabel('Y');
zlabel('Z');
% axis equal
pause(.0001)
end
axis equal
plot3(xM ,yM ,zM )
h=surf(xM ,yM ,zM ,'FaceColor','g');alpha(h,.1)