رسم صفحه در فضای سه بعدی با استفاده از فرمول دکارتی

اهمیت صفحه در فضاهای سه بعدی:

اگر شما سالیدورک کار کرده باشین، حتما متوجه شدین که مبنای رسم اشیای سه بعدی در سالیدورک، صفحه است، گاهی کل شی در یک صفحه قرار می گیرد، مثل یک نمودار فضایی و گاهی وقت‌ها،یک شی نیاز داره که در روی چند صفحه قرار بگیرد، مثل یک حجم سه بعدی یا یک رویه(پوسته فضایی)، لذا ما لازم داریم که در مرحله اول فضای سه بعدی را خلق کنیم، به عبارتی برای ساختن هر شی لازم است که اول فضای فرضی آن را معین کنیم.

صفحه هم به مانند خط دارای چندین نوع نمایش می‌باشد، که دو نوع اصلی آن نمایش دکارتی( کارتزین، صریح و..) که به فرم

ax+by+cz+d=0 و نوع دوم به فرم پارامتریک(برداری و..) است، که به فرم  زیر است:

 

دو روش بالا به راحتی به همدیگر قابل تبدیل هستند، که از این بخش می گذریم، براحتی می توانید با جستجوی «صفحه در فضا» توضیحات مفصلی دریافت کنید، اما هدف ما اینه که به یک روش ساده نمایش دکارتی صفحه را به نمایش پارامتریک آن تبدیل کنیم تا بتوانیم به سرعت صفحه مورد نظر خود را با کمترین زمان لازم، ایجاد کنیم و به اصطلاح خودمان! فضای لازم برای رسم نمودار فضایی را بسازیم.

در این تکنیک،

1- ضرایب فرمول دکارتی صفحه را پیدا می کنیم،

2-اگر ضریب z برابر صفر باشد، به سراغ ضریب  yمی‌رویم، اگر ضریب آن صفر بود به سراغ ضریب x می‌رویم.

3-اولین متغیری که در پروسه 2 دارای ضریب غیر صفر بود را به عنوان تابع و بقیه متغیرها را به عنوان متغیر در نظر می‌گیریم، مثلا  برای تابع   داریم:   

در مرحله بعد  فرایند زیر را  اجرا می کنیم:

 

 سپس برای متغیرها بازه تعریف می کنیم، مثلا p=[-2:2], q=[-3:3]  و سپسp  را عمودی و q را افقی تکرار می‌کنیم که می‌توان با استفاده از تابع meshgrid براحتی این کار را انجام داد، سپس از روی دو ماتریس ایجاد شده، می‌توانیم y را بدست بیاوریم، حالا با استفاده از دستور surf در یک مرحله یا با استفاده از دستور plot3 در دو مرحله می‌توانیم صفحه دلخواه خودمان را رسم کنیم.

نکته اول: مهم نیست ضریب متغیرها صفر باشد یا هر ضریب دیگر، فرایند بالا( دادن بازه برای متغیرها)، بی کم و کاست باید طی شود.

نکته دوم : برای تعیین یک صفحه و بدست آوردن ضرایب آن سه نقطه را روی فضای سه بعدی معین کنین و سپس بردارهای  فضایی را بسازین و بعد با ضرب خارجی بردار نرمال آن را بدست بیاورین و بعد با ضرب داخلی بردار نرمال در یکی از بردارهای روی صفحه فرمول صفحه دلخواه خود را بدست بیاورین. برای کسب اطلاعات بیشتر  می توانین به این صفحه مراجعه کنین.

حالا تمام توضیحات بالا به زبان برنامه نویسی در ادامه بازگو شده است، در کد زیر شما کافی است که فرمول دکارتی صفحه دلخواه خود را در سطر 20 کد وارد کنید.

کد اجرایی:

%% clear and close all child forms
delete(allchild(0));close all;
clear;
clc;

%% plot coordinates system in 3D area and labeling
plot3([-5;5],[-5;5]*0,[-5;5]*0,'k');hold on;
plot3([-5;5]*0,[-5;5],[-5;5]*0,'k');hold on
plot3([-5;5]*0,[-5;5]*0,[-5;5],'k');hold on
text([-6;6],[-6;6]*0,[-6;6]*0,{'-X','X'});hold on;
text([-6;6]*0,[-6;6],[-6;6]*0,{'-Y','Y'});hold on
text([-6;6]*0,[-6;6]*0,[-6;6],{'-Z','Z'});hold on
xlabel('X');
ylabel('Y');
zlabel('Z');


%% convert implicit plan formula as parametric form
syms x y z scalerVal;
plan='2*x+3*y+0*z+1';%% plan as inplicit form
pluIdex=strfind(plan,'+');%% find plus index in plan formula
scalerIndex=strsplit(plan,'+');
for s=1:length(scalerIndex)
    scalerVal=str2num(scalerIndex{s});
    if ~isempty(scalerVal)
        break;
    else
        scalerVal=0;
    end
end

%% extract z coff

zIndex=strfind(plan,'z');
if ~isempty(zIndex)
    pluIZ=pluIdex(pluIdex<zIndex);
    if ( pluIZ)
        pluIZ=pluIZ(end);
        cofZIndex=pluIZ+1:zIndex-2;
        cofZ=str2double(plan(cofZIndex));
    else
        if (zIndex>1)
            pluIZ=1;
            cofZIndex=pluIZ:zIndex-2;
            cofZ=str2double(plan(cofZIndex));
        else
            cofZ=1;
        end
    end
else
    cofZ=0;

end
%% extract y coff

yIndex=strfind(plan,'y');
if ~isempty(yIndex)
    pluIY=pluIdex(pluIdex<yIndex);
    if ( pluIY)
        pluIY=pluIY(end);
        cofYIndex=pluIY+1:yIndex-2;
        cofY=str2double(plan(cofYIndex));
    else
        if (yIndex>1)
            pluIY=1;
            cofYIndex=pluIY:yIndex-2;
            cofY=str2double(plan(cofYIndex));
        else
            cofY=1;
        end
    end
else
    cofY=0;

end
%% extract x coff
xIndex=strfind(plan,'x');
if ~isempty(xIndex)
    pluIX=pluIdex(pluIdex<xIndex);
    if ( pluIX)
        pluIX=pluIX(end);
        cofXIndex=pluIX+1:xIndex-2;
        cofX=str2double(plan(cofXIndex));
    else
        if (xIndex>1)
            pluIX=1;
            cofXIndex=pluIX:xIndex-2;
            cofX=str2double(plan(cofXIndex));
        else
            cofX=1;
        end
    end
else
    cofX=0;

end

coff=[cofX,cofY,cofZ];


funcIndex=find(coff);funcIndex=funcIndex(end);
switch funcIndex
    case 1
        y=[-2:2];
        z=[-2:2];
        [y,z]=meshgrid(y,z);
        x=-(coff(2)/coff(1))*y -(coff(3)/coff(1))*z-scalerVal/coff(1);

        
        
    case 2
        x=[-2:2];
        z=[-2:2];
        [x,z]=meshgrid(x,z);
        y=(coff(1)/coff(2))*x +(coff(3)/coff(2))*z+scalerVal/coff(2);

    case 3
        x=[-2:2];
        y=[-2:2];
        [x,y]=meshgrid(x,y);
        z=(coff(1)/coff(3))*x +(coff(2)/coff(3))*y+scalerVal/coff(3);
end


 
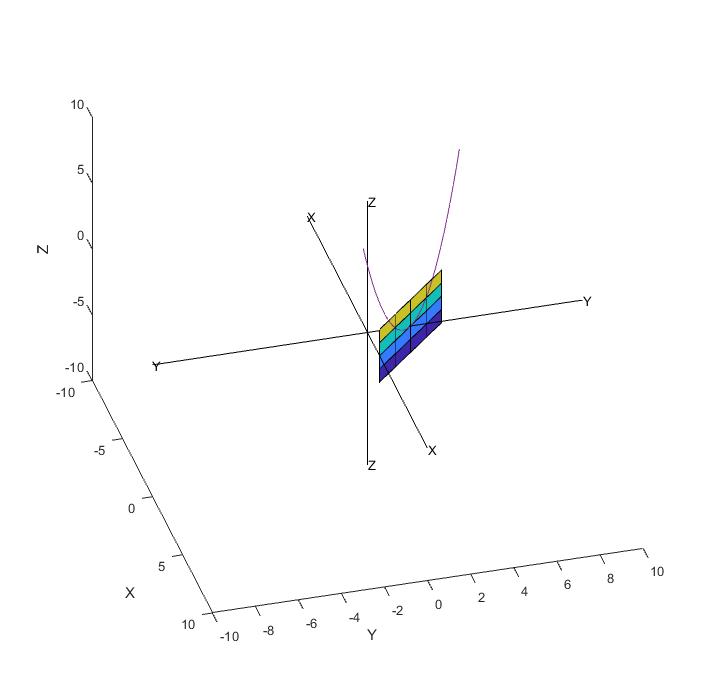
surf(x,y,z)

نمونه خروجی:

دانلود کد:

 

نحوه رسم یک نمودار در روی یک صفحه دلخواه

در این پست، کدی را قرار دادیم که در آن یک  نمودار دلخواه را در روی یک صفحه چاپ کنید، البته این یک کد مقدماتی می باشد و در پست های بعدی آموزش ایجاد یک صفحه دلخواه و چاپ یک نمودار دلخواه روی این صفحه را مفصل شرح خواهیم داد و در نهایت رشد چند ضلعلی دلخواه در راستای نمودار، حول مختصات دلخواه را عملیاتی خواهیم کرد،

این پست در حقیقت مقدمه ای هست برای توزیع نودها در فضاهای سه بعدی در درون اشیای سه بعدی .

شما می توانید تابع z را بر مبنای پارامتر t تغییر دهید مثلا z=t^2 +1 و... تا چاپ آن را روی صفحه فرضی را مشاهده کنین.

 کد  اجرایی: 

 

%% clear commands
 
delete(allchild(0));close all;
clear;
clc;


plot3([-10;10],[-10;10]*0,[-10;10]*0,'k');hold on;
plot3([-10;10]*0,[-10;10],[-10;10]*0,'k');hold on
plot3([-10;10]*0,[-10;10]*0,[-10;10],'k');hold on
text([-10;10],[-10;10]*0,[-10;10]*0,'X');hold on;
text([-10;10]*0,[-10;10],[-10;10]*0,'Y');hold on
text([-10;10]*0,[-10;10]*0,[-10;10],'Z');hold on
xlabel('X');
ylabel('Y');
zlabel('Z');
t=[-3.14:.2:3.14];
x=t;
y=-t+2;
z=sin(t );
plot3(t,-t+2,t.^2);hold on

[u,v]=meshgrid(-2:2,-2:2);
surf(u,-u+2,v)

 نمونه خروجی:

دانلود کد:

 

 

رشد دادن یک چند ضلعی در یک مسیر سینوسی روی صفحه xy

در این پست نحوه ایجاد یک شلنگ سینوسی از طریق رشد دادن چند ضلعی، در راستای یک مسیر سینوسی روی صفحه xy آورده شده است، 

توضیح مختصر: به ازای زوایای مثبت، چرخش  در خلاف عقربه های ساعت و به ازای زوایای منفی، چرخش در جهت عقربه های ساعت صورت گرفته است. از دو تابع rotateParameter برای چرخش  و  angl= anglOnePolToTwoPol(angl,type) برای تغییر زوایای دوقطبی به تک قطبی استفاده شده، مثلا 270 را به -90 درجه تبدیل می کنه( در حالی که نوع 2 باشه) و در نوع 1( رادیان)، مثلا (pi/2) *3 را به -pi/2 تبدیل می کنه.

کد اجرایی:

%% clear commands
function xx
delete(allchild(0));close all;
clear;
clc;

%% path commands
file=matlab.desktop.editor.getActive;
try
    fileDetail=dir(file.Filename);
    folderName=fileDetail.folder;
catch
    index=strfind( file.Filename,'\');
    folderName=file.Filename(1:index(end)-1);
end
paths=genpath(folderName);
addpath(paths);
cd(folderName);


side=20;
t=linspace(0,2*pi ,side+1);
side1=50;
t1=linspace(0, 2*pi ,side1+1);
ph=0;

path.x=  t1 ;
path.y= sin(t1+ph) *5  ;

plot([t1;path.x ] ,[path.y*0 ;path.y] ,'r' );hold on
plot3([-7:7]',[-7:7]'*0,[-7:7]'*0);hold on
plot3([-7:7]'*0,[-7:7]' ,[-7:7]'*0 );hold on
plot3([-7:7]'*0,[-7:7]'*0,[-7:7]' );hold on
text(7,0,0,'x');hold on
text(0,7,0,'y');hold on
text(0,0,7,'z');hold on
% [path.x,path.y]=divider(path.x,path.y,2);
% [~,t1]=divider(t1,t1,2);


fig.x= cos(t )/2  ;
fig.y=  0*(0:side);
fig.z= sin(t  )/2   ;
fig1=fig;
% plot(t1,tan(t1))

for in=1:length(path.x)-1
    plot3(fig.x+path.x(in),fig.y+path.y(in) ,fig.z ,'b-');hold on


    if (anglOnePolToTwoPol(t1(in),1)>0)
        [ fig.x, fig.y, fig.z]=rotateParameter(fig1,[0,0,1],   -rad2deg(t1(in)) );
    elseif (anglOnePolToTwoPol(t1(in),1)<0)
        [ fig.x, fig.y, fig.z]=rotateParameter(fig1,[0,0,1],  rad2deg(t1(in)) );
    end



    surf([fig.x+path.x(in);fig.x+path.x(in+1) ],[fig.y+path.y(in);fig.y+path.y(in+1) ],[fig.z;fig.z],'facecolor','k');hold on; alpha(0.2)

    view(3);
    axis('equal')
end
end

function [ newx, newy, newz]=rotateParameter(matrixObj,azel,alpha)

u = azel(:)/norm(azel);
alph = alpha*pi/180;
cosa = cos(alph);
sina = sin(alph);
vera = 1 - cosa;
x = u(1);
y = u(2);
z = u(3);
rot = [cosa+x^2*vera x*y*vera-z*sina x*z*vera+y*sina; ...
    x*y*vera+z*sina cosa+y^2*vera y*z*vera-x*sina; ...
    x*z*vera-y*sina y*z*vera+x*sina cosa+z^2*vera]';

x = matrixObj.x;
y = matrixObj.y;
z = matrixObj.z;

[m,n] = size(z);
if numel(x) < m*n
    [x,y] = meshgrid(x,y);
end

[m,n] = size(x);
newxyz = [x(:) , y(:) , z(:) ];
newxyz = newxyz*rot;
newx =   reshape(newxyz(:,1),m,n);
newy =  reshape(newxyz(:,2),m,n);
newz =  reshape(newxyz(:,3),m,n);

end



function angl= anglOnePolToTwoPol(angl,type)
if nargin==1
    type=1;
end
switch type
    case 1% radian type
        angl=mod(angl,2*pi);
        miInd=angl<0;
        angl(miInd)=(2*pi)+angl(miInd);

    case 2
        angl=mod(angl,360);
        miInd=angl<0;
        angl(miInd)=(360)+angl(miInd);
end
end

نمونه خروجی:

دانلود کد

رشد چند ضلعی حول محور z , y

 در این پست یک مقدمه ای برای رشد اشکال هندسی بسته و باز حول یک مسیر معین تشریح شده

شما می توانین متغیر side چند ضلعی رشد و مسیر را تعیین کنین و تغییرات را مشاهده کنین

رشد چند ضلعی حول محور y،

%% clear commands
function xx
delete(allchild(0));close all;
clear;
clc;

%% path commands
file=matlab.desktop.editor.getActive;
try 
fileDetail=dir(file.Filename);
folderName=fileDetail.folder;
catch
   index=strfind( file.Filename,'\');
   folderName=file.Filename(1:index(end)-1);
end
paths=genpath(folderName);
addpath(paths);
cd(folderName);

 
side=100;
t=linspace(0,2*pi ,side+1);
% t(6)=NaN;
side1=50;
t1=linspace(0, 2*pi ,side1+1);

  
 

 
% ph=0;
% x=r' *cos(t+ph);
% z=(0:side)' * ones(1,side+1);
% y=r' *sin(t+ph) ;


ph=0;
x= cos(t+ph) /5 ;
y=  0*(0:side)';  
z= sin(t+ph) /5  ;



% plot3(x,y,z);hold on

 
% path=(t1+ph).^2;path=path/max(path)
% 
%  path.x=[0,1,1,1,2,2,2,1,1,0];
%  path.y=0:length(path.x)-1;
 
 path.x=  cos (t1+ph)*5 ;  
 path.z= sin(t1+ph) *5  ;
plot3([path.x*0;path.x ] ,[path.z*0 ;path.z]*0 ,[path.z*0 ;path.z] ,'r' );hold on
 
    [path.x,path.z]=divider(path.x,path.z,2);
    [t1,t1]=divider(t1,t1,2);

%       plot(path.x ,path.y  , 'r');hold on
% xlabel( 'X'); ylabel( 'Y'); zlabel( 'Z')
 
     matrixObj.x= cos(t )  ;
    matrixObj.z=  0*(0:side)';
    matrixObj.y= sin(t  )   ;
    
for in=1:length(path.x)-1
    
    
    
    [ x, y, z]=rotateParameter(matrixObj,[0,1,0],-rad2deg(t1(in)));
    
%      path.x=  cos (t + ph(in)) ;  
%      path.y=sin (t+ ph(in) )  ;
% 
     
       plot3(x+path.x(in),y,z+path.z(in),'b-');hold on
%        surf([x+path.x(in);x+path.x(in+1) ],[y+path.y(in);y+path.y(in+1) ],[z;z],'facecolor','k');hold on; alpha(0.2)
%       plot3(x ,y ,z,'b');hold on
xlabel('x');
ylabel('y');
zlabel('z');
      view(3);
   axis('equal') 
end
 
end

function [ newx, newy, newz]=rotateParameter(matrixObj,azel,alpha)

u = azel(:)/norm(azel);
alph = alpha*pi/180;
cosa = cos(alph);
sina = sin(alph);
vera = 1 - cosa;
x = u(1);
y = u(2);
z = u(3);
rot = [cosa+x^2*vera x*y*vera-z*sina x*z*vera+y*sina; ...
    x*y*vera+z*sina cosa+y^2*vera y*z*vera-x*sina; ...
    x*z*vera-y*sina y*z*vera+x*sina cosa+z^2*vera]';

x = matrixObj.x;
y = matrixObj.y;
z = matrixObj.z;

[m,n] = size(z);
if numel(x) < m*n
    [x,y] = meshgrid(x,y);
end

[m,n] = size(x);
newxyz = [x(:) , y(:) , z(:) ];
newxyz = newxyz*rot;
newx =   reshape(newxyz(:,1),m,n);
newy =  reshape(newxyz(:,2),m,n);
newz =  reshape(newxyz(:,3),m,n);

end

نمونه خروجی:

رشد چند ضلعی حول محور z:

%% clear commands
function xx
delete(allchild(0));close all;
clear;
clc;

%% path commands
file=matlab.desktop.editor.getActive;
try 
fileDetail=dir(file.Filename);
folderName=fileDetail.folder;
catch
   index=strfind( file.Filename,'\');
   folderName=file.Filename(1:index(end)-1);
end
paths=genpath(folderName);
addpath(paths);
cd(folderName);

 
side=20;
t=linspace(0,2*pi ,side+1);
% t(6)=NaN;
side1=50;
t1=linspace(0, 2*pi ,side1+1);

  
 

 
% ph=0;
% x=r' *cos(t+ph);
% z=(0:side)' * ones(1,side+1);
% y=r' *sin(t+ph) ;


ph=0;
x= cos(t+ph) /5 ;
y=  0*(0:side)';  
z= sin(t+ph) /5  ;



% plot3(x,y,z);hold on

 
% path=(t1+ph).^2;path=path/max(path)
% 
%  path.x=[0,1,1,1,2,2,2,1,1,0];
%  path.y=0:length(path.x)-1;
 
 path.x=  cos (t1+ph)*5 ;  
 path.y= sin(t1+ph) *5  ;
plot([path.x*0;path.x ] ,[path.y*0 ;path.y] ,'r' );hold on

 
    [path.x,path.y]=divider(path.x,path.y,2);
    [t1,t1]=divider(t1,t1,2);

%       plot(path.x ,path.y  , 'r');hold on
% xlabel( 'X'); ylabel( 'Y'); zlabel( 'Z')
 
     matrixObj.x= cos(t )  ;
    matrixObj.y=  0*(0:side)';
    matrixObj.z= sin(t  )   ;
    
for in=1:length(path.x)-1
    
    
    
    [ x, y, z]=rotateParameter(matrixObj,[0,0,1],rad2deg(t1(in)));
    
%      path.x=  cos (t + ph(in)) ;  
%      path.y=sin (t+ ph(in) )  ;
% 
     
       plot3(x+path.x(in),y+path.y(in),z,'b-');hold on
%        surf([x+path.x(in);x+path.x(in+1) ],[y+path.y(in);y+path.y(in+1) ],[z;z],'facecolor','k');hold on; alpha(0.2)
%       plot3(x ,y ,z,'b');hold on

    view(3);
   axis('equal') 
end
 end
  
function [ newx, newy, newz]=rotateParameter(matrixObj,azel,alpha)

u = azel(:)/norm(azel);
alph = alpha*pi/180;
cosa = cos(alph);
sina = sin(alph);
vera = 1 - cosa;
x = u(1);
y = u(2);
z = u(3);
rot = [cosa+x^2*vera x*y*vera-z*sina x*z*vera+y*sina; ...
    x*y*vera+z*sina cosa+y^2*vera y*z*vera-x*sina; ...
    x*z*vera-y*sina y*z*vera+x*sina cosa+z^2*vera]';

x = matrixObj.x;
y = matrixObj.y;
z = matrixObj.z;

[m,n] = size(z);
if numel(x) < m*n
    [x,y] = meshgrid(x,y);
end

[m,n] = size(x);
newxyz = [x(:) , y(:) , z(:) ];
newxyz = newxyz*rot;
newx =   reshape(newxyz(:,1),m,n);
newy =  reshape(newxyz(:,2),m,n);
newz =  reshape(newxyz(:,3),m,n);

end

نمونه خروجی:

 

دانلود هر دو کد: